1.大模型入门：监督学习与线性回归

1 前言

本系列教程将带大家从零入门当下最火热的大模型领域，了解它的底层原理，知晓它如何用一堆数学公式实现对图片的识别、对自然语言的处理、甚至能与人进行对话。

AI意为人工智能，它是历史上最早提出的概念，目标是希望设计一款能够执行人类智能特征任务的机器。

而机器学习的目的就是寻找实现人工智能的方法，比如其中经典的贝叶斯、决策树、人工神经网络等等众多机器学习方法。

而当下火热的深度学习，同样也是机器学习的一种方法。

因此总的俩说，三者之间是包含关系：

graph TB
  subgraph Outer_Box["人工智能"]
    direction TB
    subgraph Middle_Box["机器学习"]
      direction TB
      subgraph Inner_Box["深度学习"]
      end
    end
  end

目前，我们所说的“机器学习”大致包含四类：监督学习、无监督学习、半监督学习、强化学习。

比如chatgpt最初便是通过监督学习的方式实现了第一个通用聊天机器人，火爆全世界。

但由于监督学习太耗费人力，所以当下更多的研究员都在研究无监督学习、半监督学习、乃至强化学习等等。

2 监督学习

所谓监督学习，实际上就是要求输入给算法的数据集有标签，通过已知的数据提高对未知数据预测的准确性。

比如当下很多APP都会有一个识图功能，它之所以能够识别图片，就在于它事先已经学习了大量类似的图片。

比如有上千种不同类型的植物，那么就需要事先为每个种类的植物准备成千上万张的图片，让算法学习这些数据、总结出长这样的植物的名字就叫这个。

这类便称为监督学习中的分类问题。

除了分类外，另外一种叫做回归问题。

它的目标同样是根据已知的数据去预测未知的数据，只不过它预测的是一个数值。

比如我们已知过去很多年的股票数据，现在就需要根据这些已知的数据让大模型预测明天的股票价格。

3 无监督学习

监督学习中的一大痛点便是需要实现准备大量带标签的数据集，也就是我们需要人为告诉算法这个是房子、那个是车子、让它在不断的学习中获取经验，在下次看到类似的东西时就能认出这是什么东西。

但问题是，现实世界中大量的数据都是无标签的，比如网上存在着非常多的未分类的图片，绝对比分类了的图片多得多，如果没有人工去标注这些每个图片里面的内容，那么上述的监督学习就无法使用这些数据。

但问题是这样的数据太多了，人工标注的成本实在是太高了。

而无监督学习的目的就是解决这个问题，其中用的最多的就是数据聚类。

形象来说，它的作用就是将一堆数据按照某种特征分为多个子类。

比如现在有红色、绿色这两种颜色的色卡图片，在我们没有人为标注的情况下，算法并不知道输入的色卡图片是什么颜色。

但是我们可以提取图图片中的某个特性，比如提取出图片色素块RGB数值中R、G、B大于200的像素分别占比是多少。

那么可以从最终统计的明显特征就是，有一种类型的色卡R大于200占比很大，另一种色卡G大于200的占比很大，这就相当于将所有色片分类成为了两种类型。

然后我们只需要最后告诉它，R大于200占比很大的叫红色、G大于200占比很大的叫做绿色 ，这样我们就实现了以极小的人工成本实现了对数据的分类。

而从上面的过程中也能看出来，这里面的关键就在于特征的选取，特征越多、越详细、那么就能把类型分的更精细，比如虽然都是红色色卡，再细分一下的话可能还会有浅红、深红等等类别。

在有了无监督学习之后，很多机器学习的流程就变成了：

graph TB
    A["原始数据(无标签)"] --> B["无监督学习(添加标签)"] --> C["监督学习(分类预测)"]

4 线性回归

接下来便是一些数学基本理论的学习，从简单的开始。

首先便是高中应该就学过的线性回归，它属于简单、但很重要的机器学习方法，是监督学习中回归部分的基石。

我们常常需要对下图中类似的一些数据进行预测：

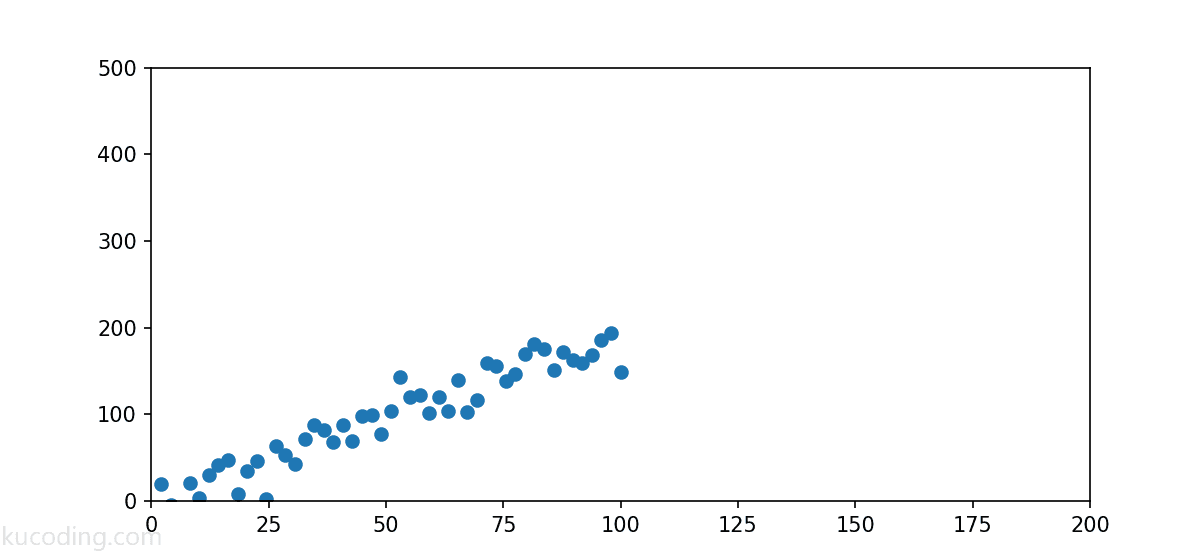
这些数据分布的很好，因为它们的整体趋势Y值是随着X轴数值增大而增大的，那么如果我们想要根据这些数据预测在x=150时，y等于多少，应该怎样预测才能充分利用这些历史数据呢？

直觉告诉我们，画一条直线、让这些散点尽可能均匀的分布在这条直线的两旁是最优的：

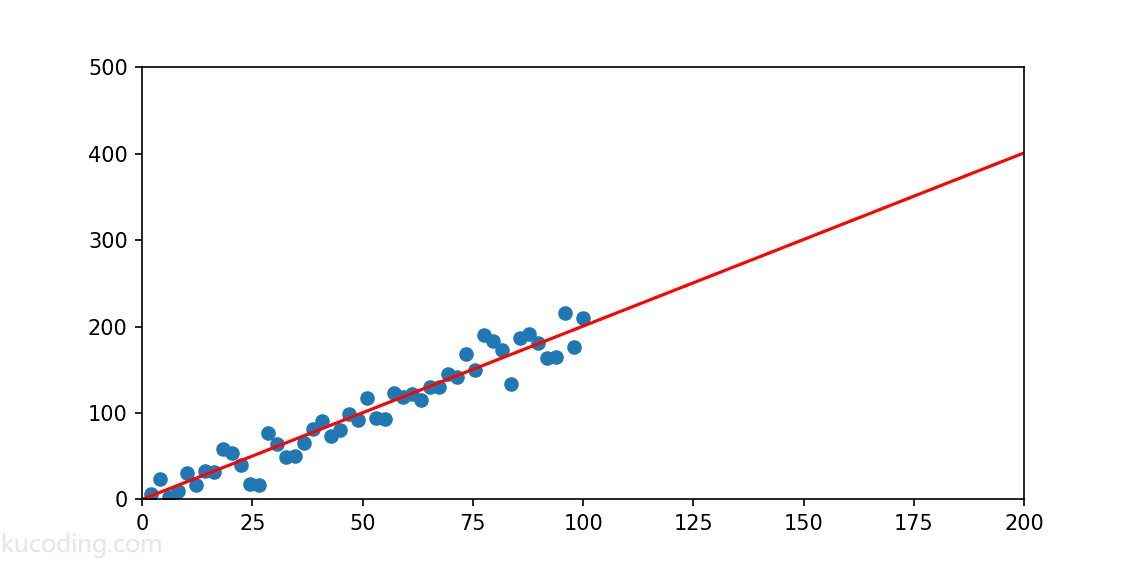
那么问题就是如何找到这条直线呢？而这便是线性回归可以做到的事情。

由于python是目前AI大模型的主流语言，所以本系列同样采用python作为示例，这些数学原理也将使用python代码演示。

4.1 uv安装与使用

推荐使用uv工具作为python的包管理器，可以省下很多麻烦事。

windows系统打开powershell运行下面命令安装uv：

powershell -ExecutionPolicy ByPass -c "irm https://astral.sh/uv/install.ps1 | iex"

如果是linux、mac系统执行下面命令安装：

curl -LsSf https://astral.sh/uv/install.sh | sh

安装完成后，创建一个新的、空目录后，执行命令：uv init

然后用vscode、cursor、trae等编辑器，打开这个目录，就可以看到当前项目已经初始化完成了：

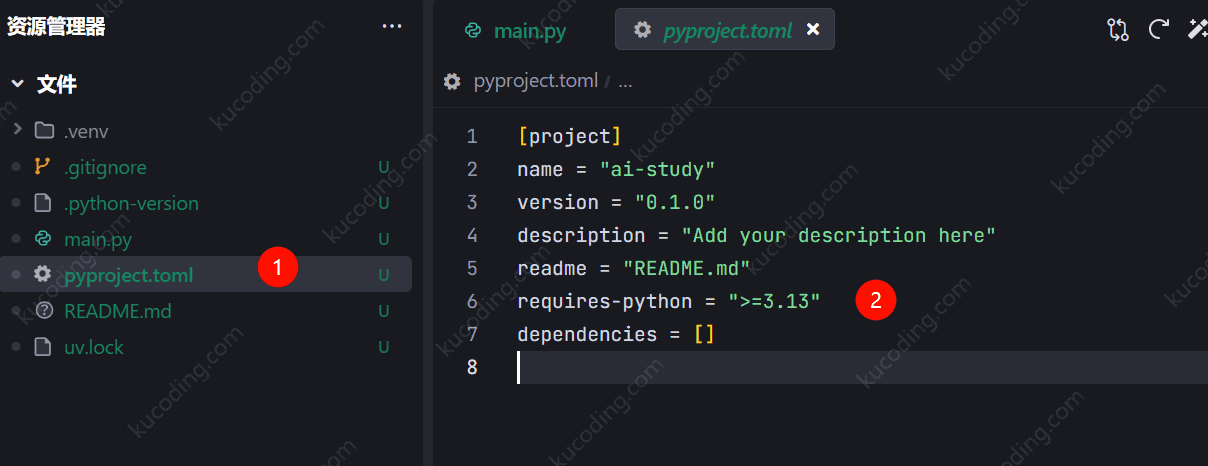
上面这个pyproject.toml就是它的配置文件，并且默认使用的是当前最新版本，对于基础学习来说直接最新的即可，但如果你后续需要调用cuda等库，可能需要修改这里的版本为3.11，最新版本cuda等库目前还没有支持。

然后我们创建一个虚拟环境，在虚拟环境中安装必要的python库：

uv venv
uv pip install matplotlib numpy

效果如下：

此时python环境就在当前项目.venv目录下，在编辑器中选择一下python编译器路径，让其能更好的给出提示信息。

输入Ctrl+shift+p快捷键，搜索python、配置其路径即可。

至此，我们的uv包管理器的python环境就搭建完成了。

其中matplotlib是python中使用范围最广的图表库，而numpy则是科学计算库，可以非常方便的让我们执行很多复杂的运算。

4.2 一元线性回归

回到前文，在搭建好了环境后，我们可以先画一下散点图：

import matplotlib.pyplot as plt
import numpy as np
def gen_data():
    xpoint = np.linspace(0, 100, 50) # 生成0-100、共50条数据的、均匀分布的数组
    y_theoretical = 2 * xpoint + 1 # 通过y=2x+1这个公式生成每个x对应的y值，这里直接是x数组中每个对应元素的计算，得到的也是一个数组
    noise = np.random.normal(0, 20, len(xpoint)) # 以0为中心点、标准差为20的正态分布算法得到一组随机数
    ypoint = y_theoretical + noisez # 让理论y值加上随机数，使其在这条直线的上下波动
    return xpoint, ypoint

xpoint, ypoint = gen_data()

plt.scatter(xpoint, ypoint) # 根据横纵坐标绘制散点图
plt.xlim(0, 200) # 设置横坐标为0-200
plt.ylim(0, 500) # 设置纵坐标为0-500
plt.show() # 显示图表

各个函数的使用已经放于代码的注释中，不理解的可以看看。

运行命令为：

uv run main.py

效果如下：

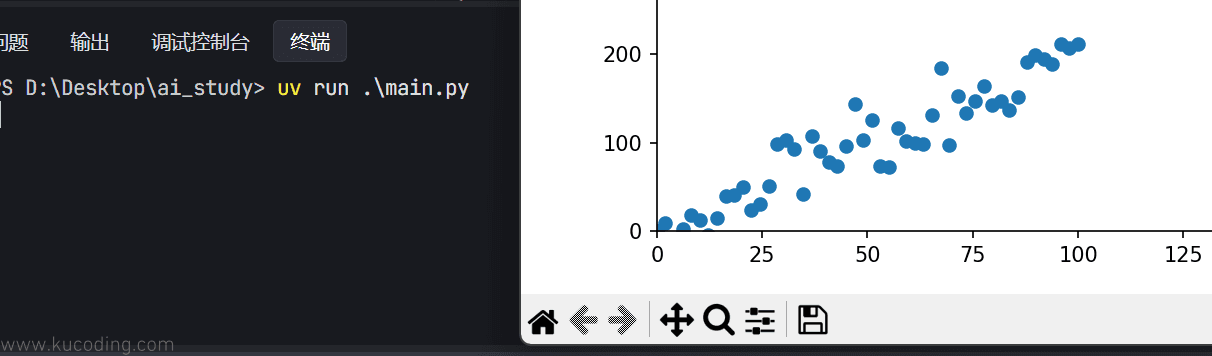
然后我们就可以在这个散点数据上进行预测了。

首先这个散点图由于是用的一元方程生成的，所以整体看上去很自然的就是一条直线，因此我们首先考虑也是一元线性回归。

$y(x)=w_0+w_1x$

上面这个公式是经典的一元一次函数表达式，通过不断组合w0与w1就能得到不同的直线。

而我们的目标就是要求出来w0与w1的数值可以让这条直线更好的拟合散点图。

而一个最直接的方式便是求每个散点到直线的y值距离的平均值，平均值越小、说明这条线越接近散点的中心、也就越拟合。

4.3 平方损失函数

举个例子，比如某个散点的坐标为$(x_i,y_i)$，那么它对应的误差就是：

$y_i-(w_0+w_1x_i)$

其中$y_i$是散点的真实坐标，而$w_0+w_1x_i$是根据公式算出来的y坐标，两者之间的差值就是根据这个公式预测出来的y值与真实的y值之间的误差，也往往被称为残差。

在机器学习中，我们更喜欢将这样的误差称之为损失，损失的越少，说明拟合的越好。

那么对于n个数据点来说，对应的损失总和就是：

$\sum_{i=1}^n (y_i-(w_0+w_1x_i))$

更进一步，为了防止出现正、负数求和、将损失消掉，我们一般会取平方和，机器学习中将其称为平方损失函数：

$\sum_{i=1}^n (y_i-(w_0+w_1x_i))^2$

python代码中实现这个函数很简单：

def square_loss(x: np.ndarray, y: np.ndarray, w0: float, w1: float):
    """平方损失函数"""
    loss = sum(np.square(y - (w0 + w1 * x)))
    return loss

由于np库的数组运算可以直接看作一个变量，其底层会自动展开为对应元素计算，所以看起来非常的简洁、不用嵌套各种循环。

只是要注意，如果要对np库的各类变量进行运算，就要使用np提供的函数，比如这里使用的是np库提供的square这函数来求平方，得到的依旧是一个数组，最后调用sum求数组的和。

4.4 最小二乘法代数求解

一般我们常用最小二乘法来求解线性回归的拟合参数，这里的二乘指的就是平方、也就是上面的平方损失函数。

首先平方损失函数为：

$f=\sum_{i=1}^n (y_i-(w_0+w_1x_i))^2$

为了求f最小的时候w0与w1的值，我们就需要对这个函数分别对w0与w1求1阶偏导：

$\frac{\partial f}{\partial w_0} = -2 \left( \sum_{i=1}^{n} y_i - n w_0 - w_1 \sum_{i=1}^{n} x_i \right)$

$\frac{\partial f}{\partial w_1} = -2 \left( \sum_{i=1}^{n} x_iy_i - w_0\sum_{i=1}^{n}x_i - w_1 \sum_{i=1}^{n} x_i^2 \right)$

注意，上面两个公式是求偏导之后、再拆分了一下的，为的是能更加方便的看清w0与w1的位置。

由于从图中我们可以看的出来，只有当直线位于散点中心时值最小、也就是这个方程有且仅有一个极小值。

因此只需要让$\frac{\partial f}{\partial w_0}=0$ 和 $\frac{\partial f}{\partial w_1}=0$之后，求出对应的w0与w1的值即可，此时它们就是极值点坐标，由于可以分析出它只有一个最小极值点，因此这个点就是最小极值点。

这里只是因为有求和函数导致看起来很复杂，实际上就是一个二元方程组：

$w_1 = \frac{n \sum x_i y_i - \sum x_i \sum y_i}{n \sum x_i^2 - \left( \sum x_i \right)^2}$

$w_0 = \frac{\sum x_i^2 \sum y_i - \sum x_i \sum x_i y_i}{n \sum x_i^2 - \left( \sum x_i \right)^2}$

注意求解过程中，不要将 $\sum_{i=1}^nx_i \sum_{i=1}^ny_i$ 与 $\sum_{i=1}^{n}x_iy_i$混为一谈、直接合并了，前者是分别求和之后的乘积，后者是乘积之和。

然后将上面的公式转换为代码就是：

def least_squares_algebraic(x: np.ndarray, y: np.ndarray):
    """最小二乘法代数求解"""
    n = x.shape[0]
    w1 = (n * sum(x * y) - sum(x) * sum(y)) / (n * sum(x * x) - sum(x) * sum(x))
    w0 = (sum(x * x) * sum(y) - sum(x) * sum(x * y)) / (
        n * sum(x * x) - sum(x) * sum(x)
    )
    return w0, w1

然后我们尝试使用这个函数来求拟合函数：

import matplotlib.pyplot as plt
import numpy as np
def gen_data():
    xpoint = np.linspace(0, 100, 50)
    y_theoretical = 2 * xpoint + 1
    noise = np.random.normal(0, 20, len(xpoint))
    ypoint = y_theoretical + noise
    return xpoint, ypoint

def least_squares_algebraic(x: np.ndarray, y: np.ndarray):
    """最小二乘法代数求解"""
    n = x.shape[0]
    w1 = (n * sum(x * y) - sum(x) * sum(y)) / (n * sum(x * x) - sum(x) * sum(x))
    w0 = (sum(x * x) * sum(y) - sum(x) * sum(x * y)) / (
        n * sum(x * x) - sum(x) * sum(x)
    )
    return w0, w1


# 散点图
xpoint, ypoint = gen_data()
plt.scatter(xpoint, ypoint)
plt.xlim(0, 200)
plt.ylim(0, 500)


# y = 2x + 1 画一条直线
x1=np.array([0,200]) #使用np设置横坐标点
y1=np.array([0,401]) #用公式手动计算出对应的y值
plt.plot(x1,y1, color='red')

# 拟合线
w0, w1 = least_squares_algebraic(xpoint, ypoint)
y2=x1*w1+w0 # 通过拟合的值计算y值
plt.plot(x1,y2, color='green')

plt.show()

效果如下，可以看到，绿色的拟合线与红色的标准线非常的接近：

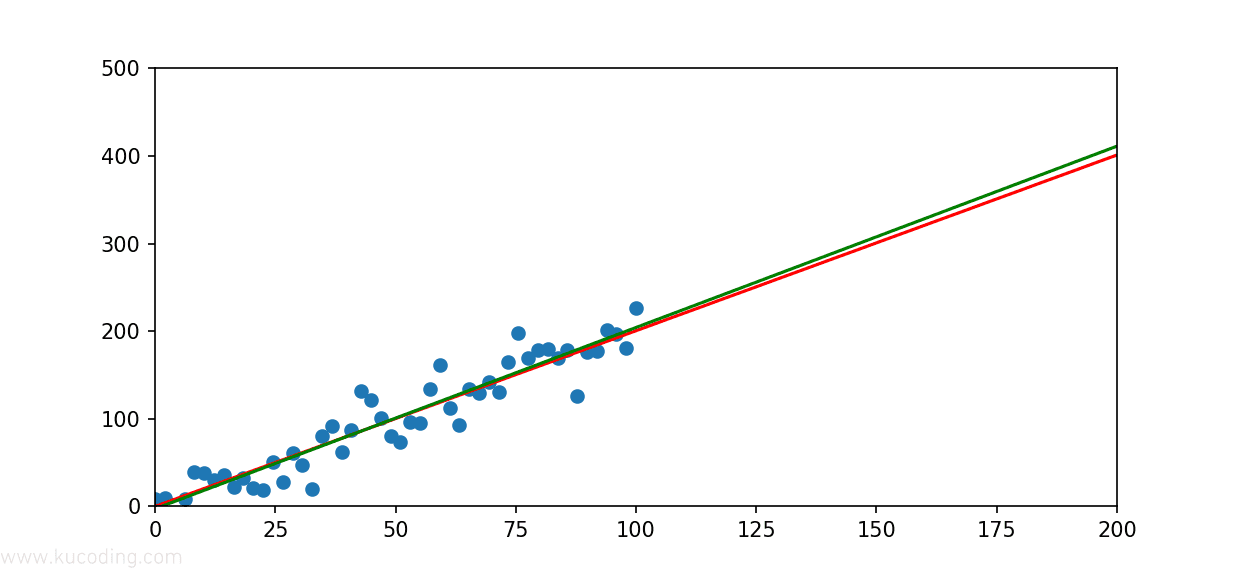
代入前面的散点图看，你甚至可能会觉得绿色的线才应该更加正确，因为它的两侧散点分布会更加均匀。

4.5 最小二乘法矩阵求解

上面代数求解的方式虽然已经很不错了，但也仅限于小数据集，比如这里只有x、y两个维度。

而实际机器学习往往有成百上千过万乃至上百万的维度，如果依旧使用上述的代数求解就会力不从心了。

所以这里引入大学课程会学到的矩阵求解，这也是目前大模型主流的运算方法。

上述的$y(x)=w_0+w_1x$表达为矩阵形式如下：

$\begin{bmatrix} 1 & x_1 \\ \vdots & \vdots \\ 1 & x_{i} \\ \vdots & \vdots \\ 1 & x_{n} \end{bmatrix} \begin{bmatrix} w_0 \\ w_1 \end{bmatrix} = \begin{bmatrix} y_2 \\ \vdots \\ y_{i} \\ \vdots \\ y_{n} \end{bmatrix}$

注意这里的表述方式发生了变化，上面代数表达式只写了一个代指任意一个数值$x_i$与$y_i$，而这里矩阵中为了让其更加好看，写了其所有的可能。

矩阵乘法原理不会、或者忘了的可以参考：矩阵乘法_百度百科

为了表述方便，这里将上面的矩阵等式转换一下：

$Y=XW$

$Y=\begin{bmatrix} y_2 \\ \vdots \\ y_{i} \\ \vdots \\ y_{n} \end{bmatrix} , X=\begin{bmatrix} 1 & x_1 \\ \vdots & \vdots \\ 1 & x_{i} \\ \vdots & \vdots \\ 1 & x_{n} \end{bmatrix} , W=\begin{bmatrix} w_0 \\ w_1 \end{bmatrix}$

所以此时，我们就可以将上述的平方损失函数转换为：

$f=\sum_{i=1}^n(y_i-(w_0+w_1x_i))^2=(Y-XW)^T(Y-XW)$

注意这里的转换逻辑，线性代码公式的含义是i=0\dots n时，求所有等式结果平方和。

因此转换为矩阵公式时，只需要计算$Y-XW$得到的就是所有i=0 \dots n公式的结果矩阵，然后再让其乘以它的转置矩阵，也就是$(Y-XW)^T$，得到的结果就是只包含一个平方和结果的1x1矩阵了。

矩阵转置方面的内容可以参考：线性代数（六）转置和置换矩阵 - 知乎。

然后对上述公式应用矩阵转置的基本定律与乘法分配律后得到结果：

$f=Y^TY-Y^T(XW)-(XW)^TY+(XW)^TXW$

由于$XW$与$Y^T$的结果都是$(n,1)$矩阵，所以$Y^T(XW)=Y(XW)^T$，上述表达式可以简化为：

$f=Y^TY-2(XW)^TY+(XW)^TXW$

然后现在的问题就是在W取什么值时，这个式子的值是最小的。

方法依旧是求导，根据矩阵的求导公式，可以得到下面这个结果：

$\frac{\partial f}{\partial W} = 2X^TXW-2X^TY=0$

进而计算得到：

$W=(X^TX)^{-1}X^TY$

如果对矩阵求导感兴趣的，可以参考下面资料：

• matrix_bp
• 矩阵求导

最简单的方法是直接截图问chatgpt公式推导过程，解释的非常详细。

对应的python代码如下：

def least_squares_matrix(x: np.matrix, y: np.matrix):
    """最小二乘法矩阵求解"""
    w = (x.T * x).I * x.T * y
    return w

此时计算方式如下：

import matplotlib.pyplot as plt
import numpy as np
def gen_data():
    xpoint = np.linspace(0, 100, 50)
    y_theoretical = 2 * xpoint + 1
    noise = np.random.normal(0, 20, len(xpoint))
    ypoint = y_theoretical + noise
    return xpoint, ypoint

xpoint, ypoint = gen_data()
plt.scatter(xpoint, ypoint)

def least_squares_algebraic(x: np.ndarray, y: np.ndarray):
    """最小二乘法代数求解"""
    n = x.shape[0]
    w1 = (n * sum(x * y) - sum(x) * sum(y)) / (n * sum(x * x) - sum(x) * sum(x))
    w0 = (sum(x * x) * sum(y) - sum(x) * sum(x * y)) / (
        n * sum(x * x) - sum(x) * sum(x)
    )
    return w0, w1

w0, w1 = least_squares_algebraic(xpoint, ypoint)
print('1:',w0, w1)
def least_squares_matrix(x: np.matrix, y: np.matrix):
    """最小二乘法矩阵求解"""
    w = (x.T * x).I * x.T * y
    return w

x_matrix = np.matrix(np.hstack((np.ones((xpoint.shape[0], 1)), xpoint.reshape(xpoint.shape[0], 1))))
y_matrix = np.matrix(ypoint.reshape(ypoint.shape[0], 1))
w_matrix = least_squares_matrix(x_matrix, y_matrix)
print('2:',w_matrix)
plt.show()

可以看到，这种方式的计算结果与上面的代数求解结果是一样的，只不过保留的小数不同而已：

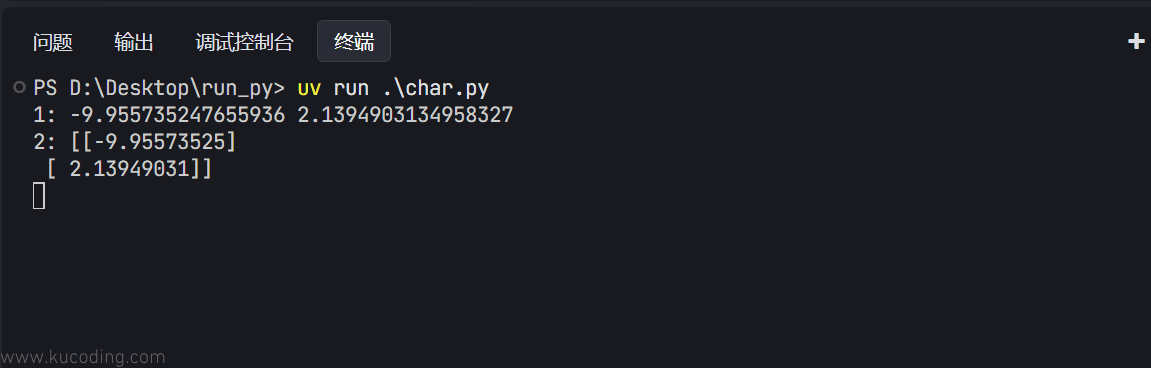
同时要注意矩阵求解时，x不再是一个一维数组，而是带上一个数字1的二维数组，代表的是前面公式中的X，也称为截距项。

代码中调用的函数解释如下：

• x.shape[0]：返回维度列表，取第一个元素，也就是第一维的长度，由于xpoint本身就是一维的，所以这里相当于获取它的长度
• xpoint.reshape：重新构建矩阵，将xpoint构建为x.shape[0]行、1列的矩阵。
• np.ones：构建一个值全为1的x.shape[0]行、1列的矩阵。
• np.hstack：组合两个m行、1列的矩阵成为为m行2列矩阵。
• np.matrix：构建matrix类型，从而拥有np库提供的各种矩阵运算函数。

4.6 scikit-learn

上面我们自己实现了相关的算法代码，但由于这类算法使用的非常频繁，所以早就有人将其封装为了库，可以让我们直接调用。

首先，安装这个开源算法库：

uv pip install scikit-learn

这个库中的LinearRegression类可以非常方便的实现线性回归计算：

sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=1)

• fit_intercept: 默认为 True，计算截距项。
• normalize: 默认为 False，不针对数据进行标准化处理。
• copy_X: 默认为 True，即使用数据的副本进行操作，防止影响原数据。
• n_jobs: 计算时的作业数量。默认为 1，若为 -1 则使用全部 CPU 参与运算。

使用实例如下：

import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression

def gen_data():
    xpoint = np.linspace(0, 100, 50)
    y_theoretical = 2 * xpoint + 1
    noise = np.random.normal(0, 20, len(xpoint))
    ypoint = y_theoretical + noise
    return xpoint, ypoint

xpoint, ypoint = gen_data()
plt.scatter(xpoint, ypoint)


# 定义线性回归模型
model = LinearRegression()
model.fit(xpoint.reshape(xpoint.shape[0], 1), ypoint)  # 训练, reshape 操作把数据处理成 fit 能接受的形状
print('1：',model.intercept_,model.coef_)

def least_squares_matrix(x: np.matrix, y: np.matrix):
    """最小二乘法矩阵求解"""
    w = (x.T * x).I * x.T * y
    return w

x_matrix = np.matrix(np.hstack((np.ones((xpoint.shape[0], 1)), xpoint.reshape(xpoint.shape[0], 1))))
y_matrix = np.matrix(ypoint.reshape(ypoint.shape[0], 1))
w_matrix = least_squares_matrix(x_matrix, y_matrix)
print('2:',w_matrix)
plt.show()

可以看到，此时得到的结果依旧是相同的：

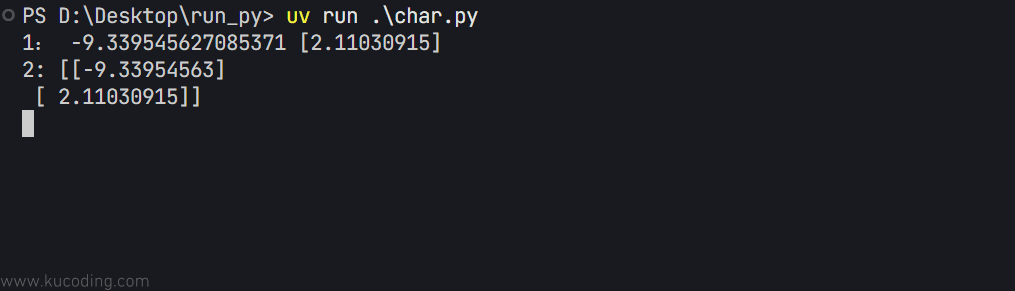
至于预测数据，直接调用它的predict函数即可，传入正确格式（这里是1行1列的二维数组）的x值：

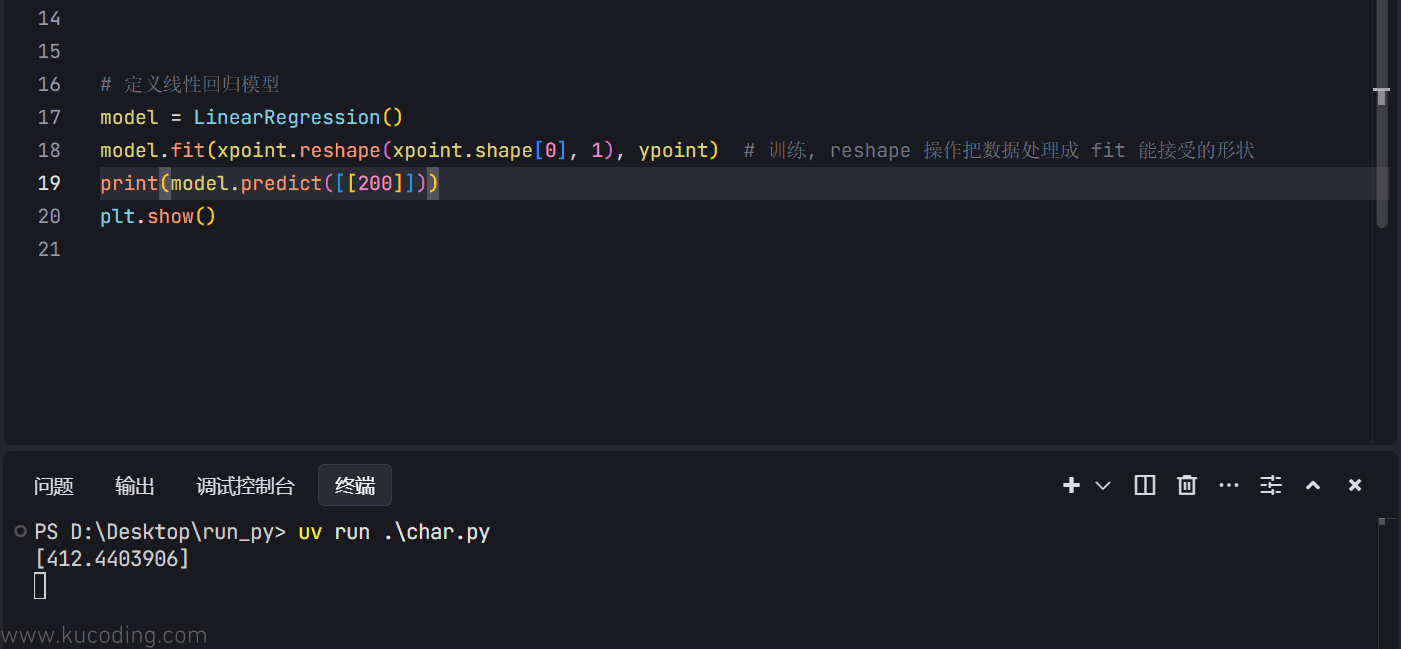
得到的结果基本符合，因为原函数本就是2x+1的附近浮动，这里也就是401的附近，属于正常预测值。

5 房价预测

这里使用上面的方式对一个经典的波士顿房价数据集进行预测，有关介绍内容可以参考官网：Boston Dataset。

也可以直接在本站下载该数据集：dataset

其内包含了很多维度的数据：

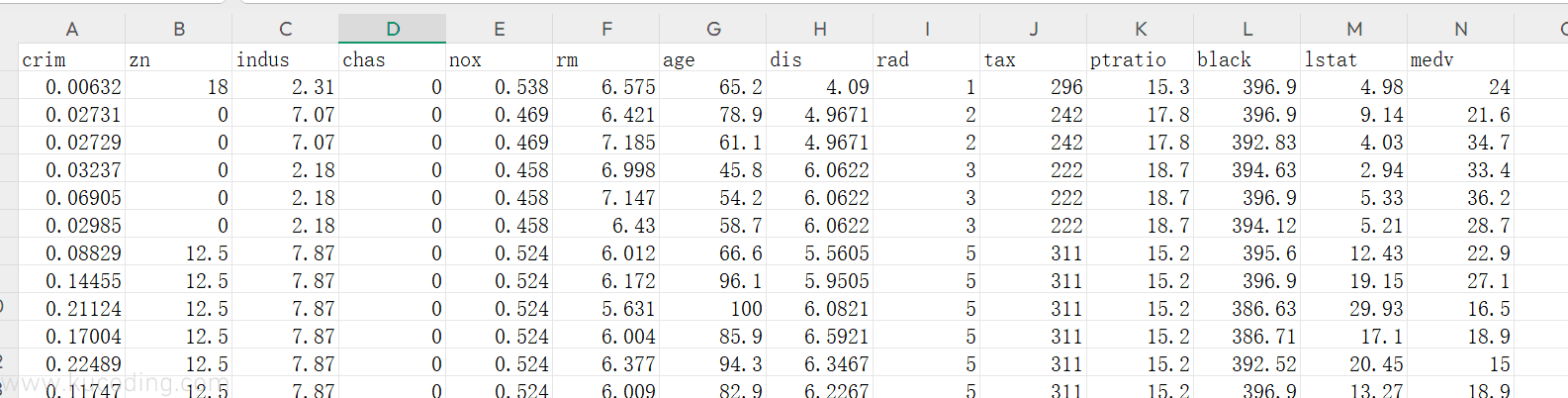
各列含义如下：

• crim: 城镇犯罪率。
• zn: 占地面积超过 2.5 万平方英尺的住宅用地比例。
• indux: 城镇非零售业务地区的比例。
• chas: 查尔斯河是否经过 (=1 经过，=0 不经过)。
• nox: 一氧化氮浓度（每 1000 万份）。
• rm: 住宅平均房间数。
• age: 所有者年龄。
• dis: 与就业中心的距离。
• rad: 公路可达性指数。
• tax: 物业税率。
• ptratio: 城镇师生比例。
• black: 城镇的黑人指数。
• lstat: 人口中地位较低人群的百分数。
• medv: 城镇住房价格中位数。

然后我们随意拿出其中三列数据进行预测，比如crim、nox、rm，预测的结果为medv。

首先，安装panda库来简单看一下这些数据的整体趋势：

uv pip install pandas

代码如下：

import pandas as pd

df = pd.read_csv("boston_data.csv")
features=df[['crim','nox','rm','medv']]
print(features.describe())

结果如下：

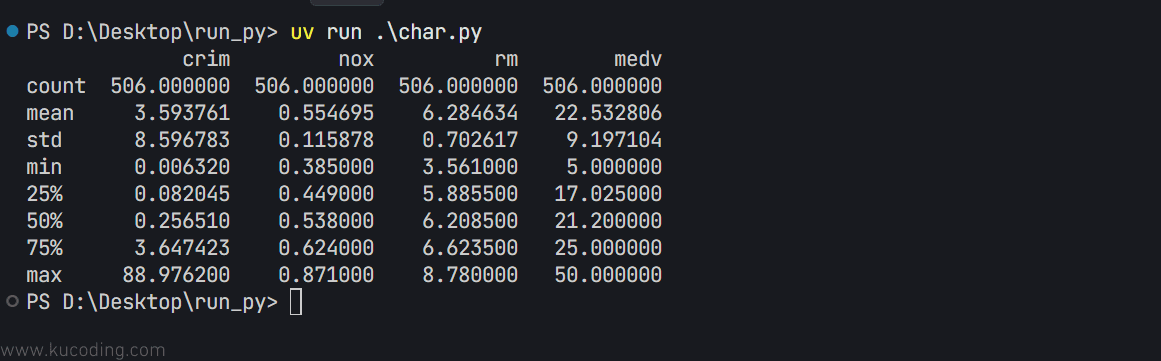
一般来说，对于测试数据，我们会用其中7成的数据用来训练模型，而剩下三成的数据则用来验证模型预测的准确度。

所以下面就以这三列数据为自变量、medv列为因变量，来训练模型试试效果：

import pandas as pd
from sklearn.linear_model import LinearRegression
df = pd.read_csv("boston_data.csv")
features=df[['crim','nox','rm']]
target = df["medv"]  # 目标值数据
split_num = int(len(features) * 0.7)  # 得到 70% 位置
X_train = features[:split_num]  # 训练集特征
y_train = target[:split_num]  # 训练集目标

X_test = features[split_num:]  # 测试集特征
y_test = target[split_num:]  # 测试集目标

model=LinearRegression()
model.fit(X_train,y_train) # 训练模型

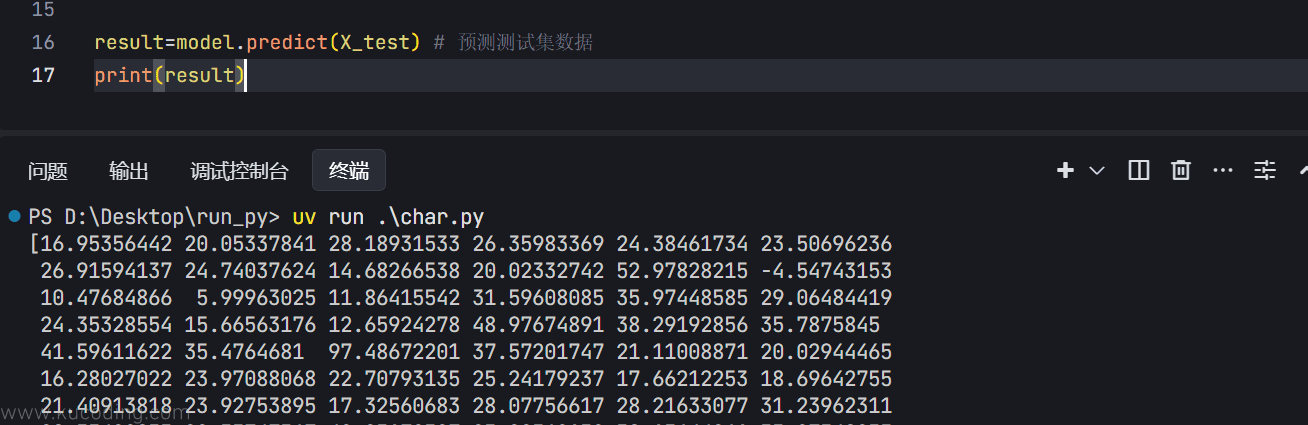
result=model.predict(X_test) # 预测测试集数据
print(result)

代码与上面是一样的，只不过这里是从文件中读取、然后7/3分成为了训练数据与测试数据、并且因变量x有三个，之前只有一个，但使用方式都是一样的，最后就能通过这三个数据预测出使用测试数据的medv的值：

有了预测数据之后，下一步要做的就是验证这些预测出来的数据是否准确。

通常我们使用的方式有平均绝对误差、均分误差等等。

其中平均绝对误差公式如下：

$\mathrm{MAE}(y, \hat{y}) = \frac{1}{n} \sum_{i=1}^{n} \left| y_i - \hat{y}_i \right|$

简单来说，就是每个预测出来的值都要与真实值做一次减法求误差的绝对值，最后整体求和、求平均得到一个平均值，这个值越小，说明预测的效果就越好。

对应的python代码如下：

def mae_solver(y_true: np.ndarray, y_pred: np.ndarray):
    """MAE 求解"""
    n = len(y_true)
    mae = sum(np.abs(y_true - y_pred)) / n
    return mae

至于均方误差，则表示误差的期望值，公式如下：

$\mathrm{MSE}(y, \hat{y}) = \frac{1}{n} \sum_{i=1}^{n} \left( y_i - \hat{y}_i \right)^2$

与上面稍微有点区别的是，这里不是取绝对值，而是直接平方。

同样的，这个值越小，说明预测的效果就越好。

相应的python代码如下：

def mse_solver(y_true: np.ndarray, y_pred: np.ndarray):
    """MSE 求解"""
    n = len(y_true)
    mse = sum(np.square(y_true - y_pred)) / n
    return mse

同样的，库里面也有现成的函数可以直接使用：

from sklearn.metrics import mean_absolute_error, mean_squared_error

完整代码如下：

import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, mean_squared_error
import numpy as np

df = pd.read_csv("boston_data.csv")
features=df[['crim','nox','rm']]
target = df["medv"]  # 目标值数据
split_num = int(len(features) * 0.7)  # 得到 70% 位置
X_train = features[:split_num]  # 训练集特征
y_train = target[:split_num]  # 训练集目标

X_test = features[split_num:]  # 测试集特征
y_test = target[split_num:]  # 测试集目标

model=LinearRegression()
model.fit(X_train,y_train) # 训练模型

result=model.predict(X_test) # 预测测试集数据

def mse_solver(y_true: np.ndarray, y_pred: np.ndarray):
    """MSE 求解"""
    n = len(y_true)
    mse = sum(np.square(y_true - y_pred)) / n
    return mse

def mae_solver(y_true: np.ndarray, y_pred: np.ndarray):
    """MAE 求解"""
    n = len(y_true)
    mae = sum(np.abs(y_true - y_pred)) / n
    return mae

print(mean_absolute_error(y_test,result),mean_squared_error(y_test,result))
print(mae_solver(y_test,result),mse_solver(y_test,result))

结果为：

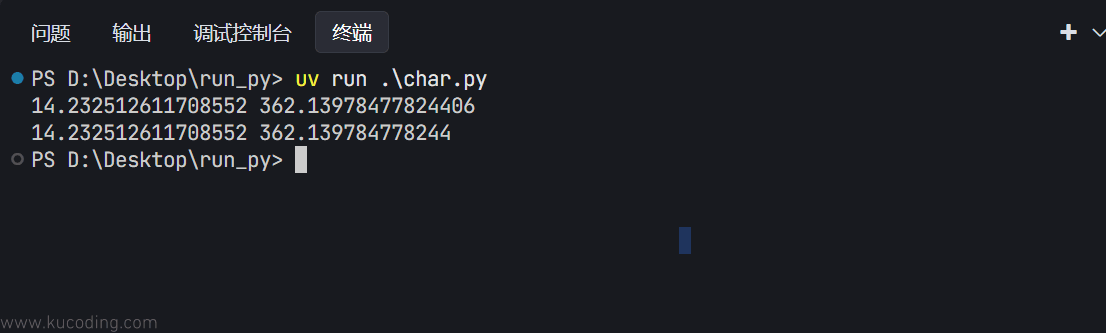
可以看到，两者的计算结果是一致的。

但我们前面看到，结果的平均值都是22左右，这里平均绝对误差居然就有14，效果非常不好。

出现这个问题的原因主要有两个：

1. 没有对数据进行预处理、剔除掉异常数据、规范数据，没有合理利用数据集中提供的其它数据，只随机选取了三个数据。
2. 线性回归算法本身并不能很好的反映房价的变化关系，房价是上下不断震荡的，难以用一条直线去预测。

后文我们会学习更多方法来提高房价的预测精度。

6 总结

通过本章的内容，我们大致理解、以及能够简单应用监督学习中的预测方法，对数据集进行训练、以及预测，学习了基本的平方损失函数的使用。

总结来说，机器学习过程往往都包含了训练于预测两部分，训练好的模型可用于对未知数据的预测，训练模型的过程，实际上就是用机器学习算法解决问题的过程，其中用到的平方损失函数、实际上就是其中的损失函数，这个函数的定义很大程度上决定了一个模型最终效果的优劣。

后续，我们也会重点介绍各类损失函数的使用。