2. 多项式回归详解：从原理推导到实战预测

1 前言

在上一章节，我们学习了如何使用线性回归对数据进行预测，但发现一元线性回归并不能很好的反应某些数据。

因此本章将要继续学习更高级的内容，让我们拥有回归预测不那么线性的数据，也就是多项式回归。

所谓多项式，指的是由变量和系数常量通过有限次加减乘除以及自然幂次的乘方运算得到的表达式，是整式的一种。

当未知数只有一个时，就被成为一元多项式，也就是上一章节所介绍的内容，比如$x^2-x+4$。

而未知数不止一个的多项式就称为多元多项式，例如$x^3-3xy^2z-yz+1$就是一个三元多项式。

2 认识多项式

为了更加直观的演示，首先这里提供一组数据，然后将其画出来：

from matplotlib import pyplot as plt

x = [4, 7, 13, 26, 31, 41, 59, 62, 71, 78]
y = [21, 35, 49, 54, 43, 30, 31, 48, 66, 74]

plt.scatter(x, y)
plt.show()

效果如下：

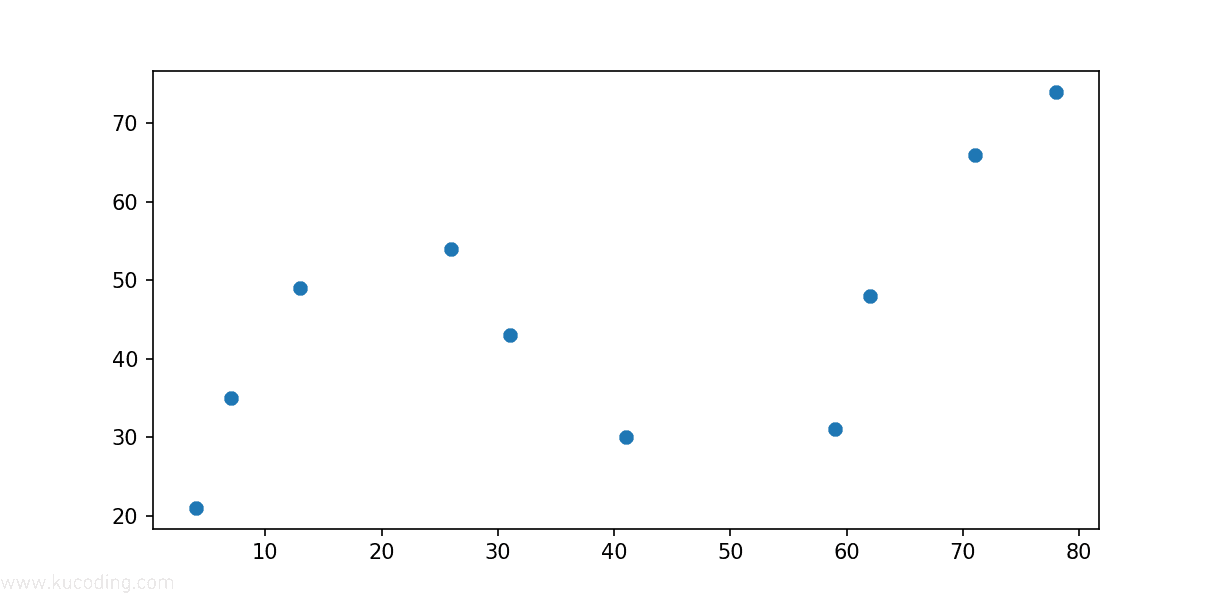
很明显可以看出来，这组数据具有明显的波动性，如果用前面学过的内容、用直线去拟合这组数据肯定效果不好。

因此下面我们来尝试使用多项式来拟合数据，首先尝试用二次多项式。

一个标准的一元高阶多项式函数如下：

$y(x, \mathbf{w}) = w_0 + w_1 x + w_2 x^2 + \cdots + w_m x^m = \sum_{j=0}^{m} w_j x^j$

其中m代表多项式的阶数，$x^j$表示x的j次幂，w代表x的系数。

因此当我们尝试用上面的一元高阶多项式去拟合数据时，就需要确定多项式系数w与阶数m，这是多项式的两个基本要素。

由于阶数我们可以实现尝试确定、比如这里设定阶数为2，那么就只需要求解系数w即可：

$y(x, \mathbf{w}) = w_0 + w_1 x + w_1 x^2$

此时，我们又回到了前面的内容，依旧是自定义损失函数：

def func(p, x):
    # 根据公式，定义 2 次多项式函数
    w0, w1, w2 = p
    x = np.asarray(x)
    f = w0 + w1 * x + w2 * x**2
    return f


def err_func(p, x, y):
    # 残差函数（观测值与拟合值之间的差距）
    f=func(p,x)
    return f-y

然后调用求解最佳拟合参数的函数即可：

from scipy.optimize import least_squares
#...
res=least_squares(err_func,[0,0,0],args=(x,y))

这里使用了scipy库内部的least_squares函数，通过最小二乘法求解最佳拟合参数，而无需自己去手动实现。

如果不存在该库可能需要自己安装一下：

uv pip install scipy

除非你需要更多自定义行为，否则只需要上面三个参数即可：损失函数、初始系数值、训练数据。

这里为了简单，直接设置了三个0作为初始值，该值并不影响结果，但它会影响最终最终多项式的次数，所以这里涉及三个，代表求解2次多项式（0、1、2次共三个系数）。

下面是一个完整的实例程序：

import numpy as np
from matplotlib import pyplot as plt
from scipy.optimize import least_squares
x = [4, 7, 13, 26, 31, 41, 59, 62, 71, 78]
y = [21, 35, 49, 54, 43, 30, 31, 48, 66, 74]

def func(p, x):
    w0, w1, w2 = p
    x = np.asarray(x)
    f = w0 + w1 * x + w2 * x**2
    return f
def err_func(p,x,y):
    f=func(p,x)
    return f-y

res=least_squares(err_func,[0,0,0],args=(x,y))

tmp_x=np.linspace(0,100,1000)
tmp_y=func(res.x,tmp_x)
plt.plot(tmp_x, tmp_y, 'r-', label='Fitted Curve')

plt.scatter(x, y)
plt.show()

得到结果的res上的x字段便是求解得到了拟合系数，然后这里生成了一组0-100共1000个数据作为横坐标、再通过该系数、横坐标计算得到纵坐标，将其画出来。

效果如下：

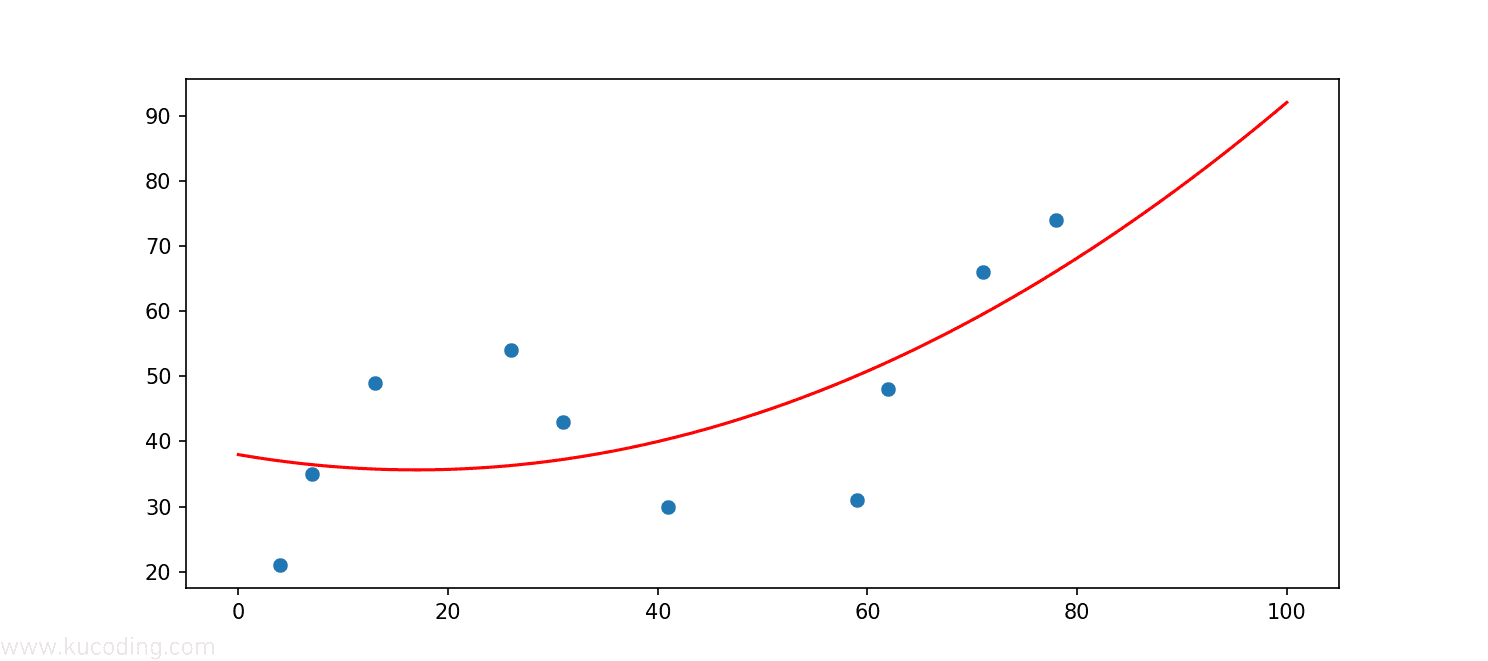
可以看到，此时拟合曲线已经出现了弯曲，但和数据点的拟合效果却并不好，这说明一元二次项依旧无法正确的反应数据点的变化趋势。

3 n次多项式

此时的方式自然就是增加拟合方程的次数了，二次不行，那就三次、四次，直到能正确拟合数据。

为了简化这个步骤，这里封装一个n次多项式的代码：

import numpy as np
from matplotlib import pyplot as plt
from scipy.optimize import least_squares
x = [4, 7, 13, 26, 31, 41, 59, 62, 71, 78]
y = [21, 35, 49, 54, 43, 30, 31, 48, 66, 74]

def fit_func(p, x):
    """根据公式，定义 n 次多项式函数"""
    f = np.poly1d(p)
    return f(x)


def err_func(p, x, y):
    """残差函数（观测值与拟合值之间的差距）"""
    ret = fit_func(p, x) - y
    return ret


def n_poly(n):
    """n 次多项式拟合"""
    p_init = np.random.randn(n)  # 生成 n 个随机数
    parameters = least_squares(err_func, p_init, args=(np.array(x), np.array(y)))
    return parameters.x


# 绘制拟合图像时需要的临时点
x_temp = np.linspace(0, 100, 1000)

# 绘制子图
fig, axes = plt.subplots(2, 3, figsize=(15, 10))

axes[0, 0].plot(x_temp, fit_func(n_poly(4), x_temp), "r")
axes[0, 0].scatter(x, y)
axes[0, 0].set_title("m = 3")

axes[0, 1].plot(x_temp, fit_func(n_poly(5), x_temp), "r")
axes[0, 1].scatter(x, y)
axes[0, 1].set_title("m = 4")

axes[0, 2].plot(x_temp, fit_func(n_poly(6), x_temp), "r")