3. 岭回归与LASSO回归详解

1 前言

除了前文提到的线性回归与多项式回归外，还有很多其它的回归方法，例如本文将要介绍的：岭回归、LASSO回归。

不过它们并没有完全创建一个新的算法进行回归，而是对我们已经使用过的最小二乘法进行某些方面的改进。

由于在上一章节中我们认识到、多项式回归其实可以看作一种特殊的线性回归形式，依旧可以使用线性回归的求解方式进行求解，因此这两种算法对多项式回归求解也是有效的。

2 最小二乘法的局限性

既然有新算法想要改进最小二乘法，那么说明这个最小二乘法肯定有某些地方不太好。

所以我们先来了解一下最小二乘法的局限性，然后再看看新的两种算法做出了哪些改进。

首先在线性回归中，我们需要求解下面这个式子：

$f(x)=\sum_{i=1}^m{w_i}x_i=w^Tx$

而最小二乘法将上面的式子改写为了：

$F=\sum_{i=1}^n(y_i-w^Tx)^2$

目的变成了求解F的最小值，前面章节中我们将其改写为了矩阵，这里我们可以将其改写为向量：

$F = \left\| Y - Xw \right\|_2^2$

式子中右下标的2代表 2-范数，是线性代数中常用的向量范数之一，它的含义是定义向量所有分量的平方和的平方根，再加上右上角的平方，最终结果就是平方和，和上面的最小二乘法表达的意思一样。

其中Y、X是所有$y_i$、$x_i$ 的集合的列向量，同时根据前文第一章得到的结论公式：

$w=(X^TX)^{-1}X^TY$

注意这个结论公式成立的条件是$|X^TX|$ 不能为0。

而问题是，当多个特征向量数值高度相关时，会导致这个结果无限趋近于0，从而导致拟合结果不稳定，间接导致过拟合风险的发生。

比如一个简单的例子：

$X = \begin{bmatrix} 1 & 2 \\ 2 & 4.001 \\ 3 & 6.002 \\ \end{bmatrix}$

这个例子中相当于有两个特征（两列）、三条数据（三行）。

可以看到，此时这两个特征数值高度相关，第二个特征值基本就是第一个特征值的两倍。

那么将其代入前面的公式：

X = \begin{bmatrix} 1 & 2 & 3 \\ 2 & 4.001 & 6.002 \\ \end{bmatrix} \cdot \begin{bmatrix} 1 & 2 \\ 2 & 4.001 \\ 3 & 6.002 \\ \end{bmatrix} = \begin{bmatrix} 1^2 + 2^2 + 3^2 & 1×2 + 2×4.001 + 3×6.002 \\ 1×2 + 2×4.001 + 3×6.002 & 2^2 + 4.001^2 + 6.002^2 \\ \end{bmatrix}

计算得：

$X^T X \approx \begin{bmatrix} 14 & 28.009 \\ 28.009 & 56.036 \\ \end{bmatrix}$

最后计算行列式的值：

$|X^T X| = 14 \cdot 56.036 - (28.009)^2 = 784.504 - 784.504081 \approx -0.000081$

可以看到，非常趋近于0。

而这便是普通最小二乘法的局限性。

2.1 皮尔卡系数

我们可以通过皮尔逊相关系数来描述这样的相关性，值越接近1代表相关性系数越高，越接近0代表相关性系数越低，如果接近-1，则代表负相关系数高。

import numpy as np
import pandas as pd
data = np.column_stack([[1, 2, 3], [2, 3.601, 6.2], [14.1, 22.1, 13.3]])
ret = pd.DataFrame(data).corr()
print(ret.round(6))

为了更好的看出效果，这里的数据集取了三个特征，也就是三列，然后取了三个数据点，也就是三行，通过corr函数即可计算出相关系数：

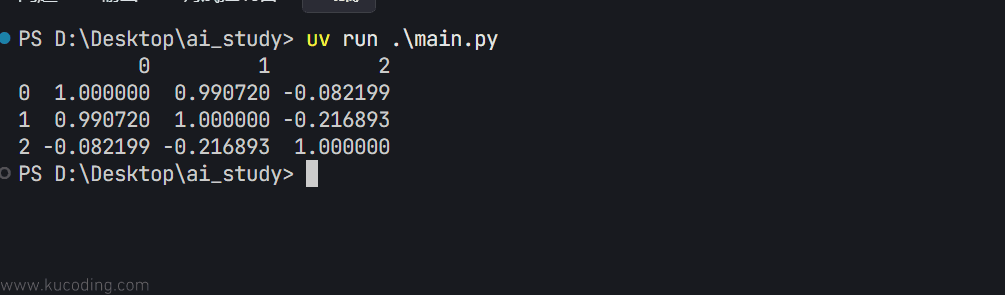
可以看到，特征0列与特征1列的数据高度相关，非常趋近于1，而特征2列随便写的数据，0列与1列的数据与之相关度都不高、趋近于0。

2.2 希尔伯特矩阵

为了能快速获取到示例数据、而不是像上面这样手写，这里再介绍一下希尔伯特矩阵，它是一种系数都是单位分数的矩阵：

$H_5 = \begin{bmatrix} 1 & \frac{1}{2} & \frac{1}{3} & \frac{1}{4} & \frac{1}{5} \\ \frac{1}{2} & \frac{1}{3} & \frac{1}{4} & \frac{1}{5} & \frac{1}{6} \\ \frac{1}{3} & \frac{1}{4} & \frac{1}{5} & \frac{1}{6} & \frac{1}{7} \\ \frac{1}{4} & \frac{1}{5} & \frac{1}{6} & \frac{1}{7} & \frac{1}{8} \\ \frac{1}{5} & \frac{1}{6} & \frac{1}{7} & \frac{1}{8} & \frac{1}{9} \end{bmatrix}$

第i行j列的系数为：

$H_{ij}=\frac{1}{i+j-1}$

这种矩阵可以直接函数生成，并且相关系数也非常高：

import pandas as pd
from scipy.linalg import hilbert
data = hilbert(3)
ret = pd.DataFrame(data).corr()
print(ret)

效果如下：

2.3 最小二乘法拟合

对于上面这种希尔伯特矩阵，假设其x_1\dots x_10服从线性分布：

y=w_1x_1+w_2*x_2+\dots+w_5*x_{10}

那么其用最小二乘法拟合的代码如下：

import numpy as np