4. 逻辑回归原理详解与python实现

1 前言

逻辑回归又叫做逻辑斯蒂回归，是机器学习中非常基础的分类方法，算法简单而高效，在实际场景中得到了广泛应用。

相比于前面章节学习的线性回归，逻辑回归是一种分类方法、而不是预测方法。

2 线性可分与不可分

一般来说，如果我们可以用一条直线在数据集中将样本数据分开，那么就称其为线性可分，否则就是线性不可分。

一个简单的例子如下：

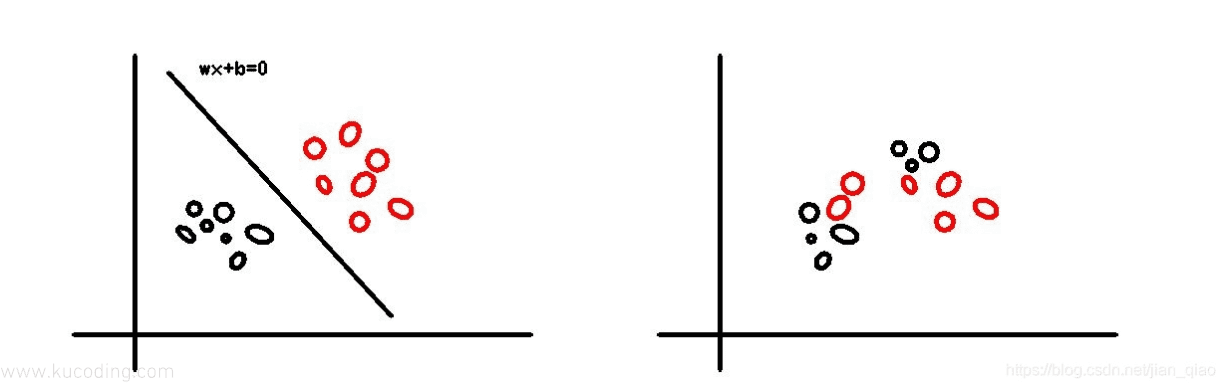
上图中，左边就可以用一条直线将样本点分为两类，但右边不行。

实际场景中的例子，比如成绩合格与不合格就是线性可分的：

import numpy as np
import matplotlib.pyplot as plt

scores = [79, 38, 91, 35, 70, 74, 67, 12, 61, 11]
passed = [1, 0, 1, 0, 1, 1, 1, 0, 1, 0]
plt.scatter(scores, passed)

# 用线性预测
model = LinearRegression()
model.fit(np.array(scores).reshape(len(scores), 1), passed)
plt.plot(scores, model.predict(np.array(scores).reshape(len(scores), 1)),color="r")


plt.xlabel("scores")
plt.ylabel("passed")
plt.show()

上面的代码中有十个成绩数据，如果大于60则认为通过，对应的值就是1，否则就是0未通过。

然后有了这个分数作为自变量、是否通过作为因变量，那么我们就可以根据这个变化来使用前面的线性回归拟合来尝试画出这条分类的线条：

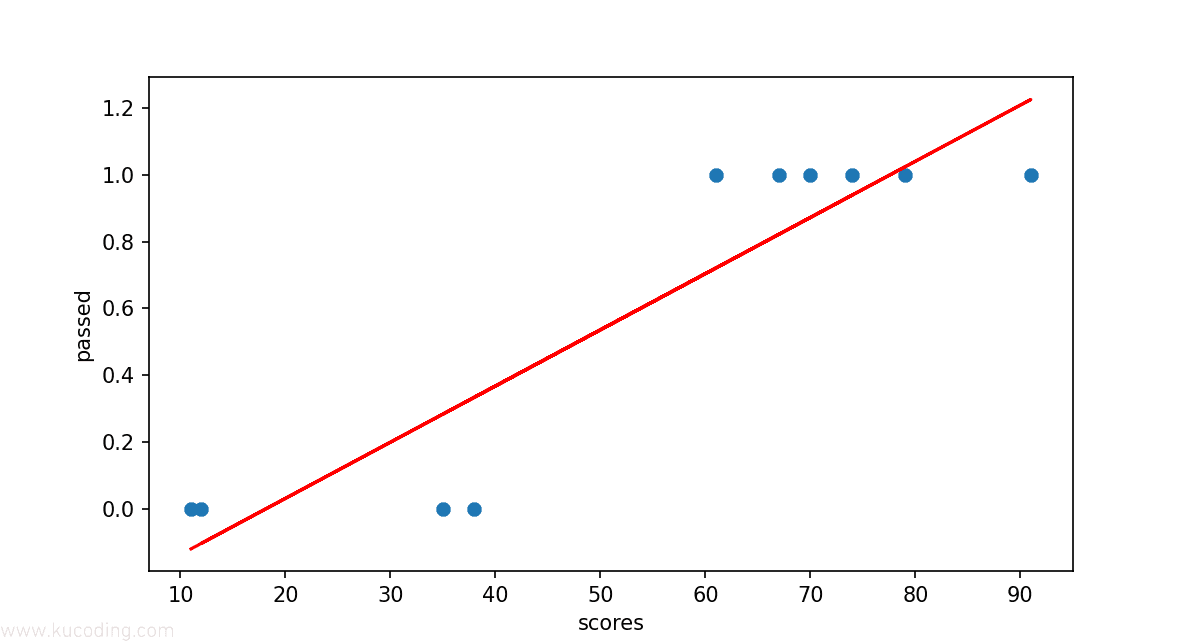
按照我们的规则，如果$x>60$，那么$f(x)>0.5$，四舍五入一下就能得到及格的1与不及格的0。

这么来看，上面这条线确实能完成基本的预测功能，只不过看起来不雅观，因为它并没有将两种类型直接划分到它的两边。

而实际上，用这种方式在某些情况下也并不能正常的进行分类划分、会出现错误的情况：

比如下面这段代码：

import numpy as np
import matplotlib.pyplot as plt

scores = [1, 2, 2, 3, 3, 3, 4, 4, 5, 6, 6, 7, 7, 8, 8, 8, 9, 9, 10]
passed = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1]
plt.scatter(scores, passed)

# 用线性预测
model = LinearRegression()
model.fit(np.array(scores).reshape(len(scores), 1), passed)
plt.plot(scores, model.predict(np.array(scores).reshape(len(scores), 1)), color="r")


plt.xlabel("scores")
plt.ylabel("passed")
plt.show()

这里的对应关系并没有那么直接，并非只要数值大于某个数，就认为它是通过的，这可以反应为某些课程的通过标准并不一致，现在拿到了这个结果、需要对其进行分类，将合格与不合格的数据分割开来。

那么此时就会出现问题：

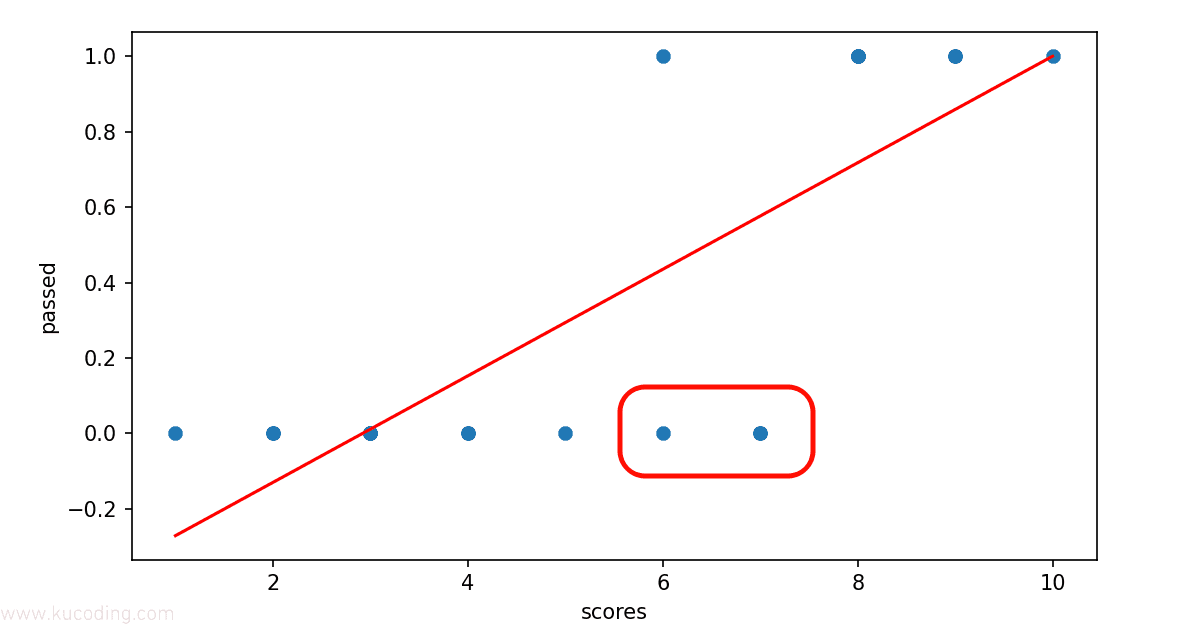
因为按照这条直线来说，x等于6、7时，y值是大于0.5的，那么就会将其归于通过，但实际上它并没有通过，这便是分类错误。

3 Sigmoid分布函数

可以看到，上面通过线性回归的方式对数据集进行分类，只适用于规则单一、呈线性变化的数据集中，否则很容易出现分类错误。

而且在上述这类$0-1$分类问题中，用线性回归还可能出现负数、大于1的数，这都不是我们想要的。

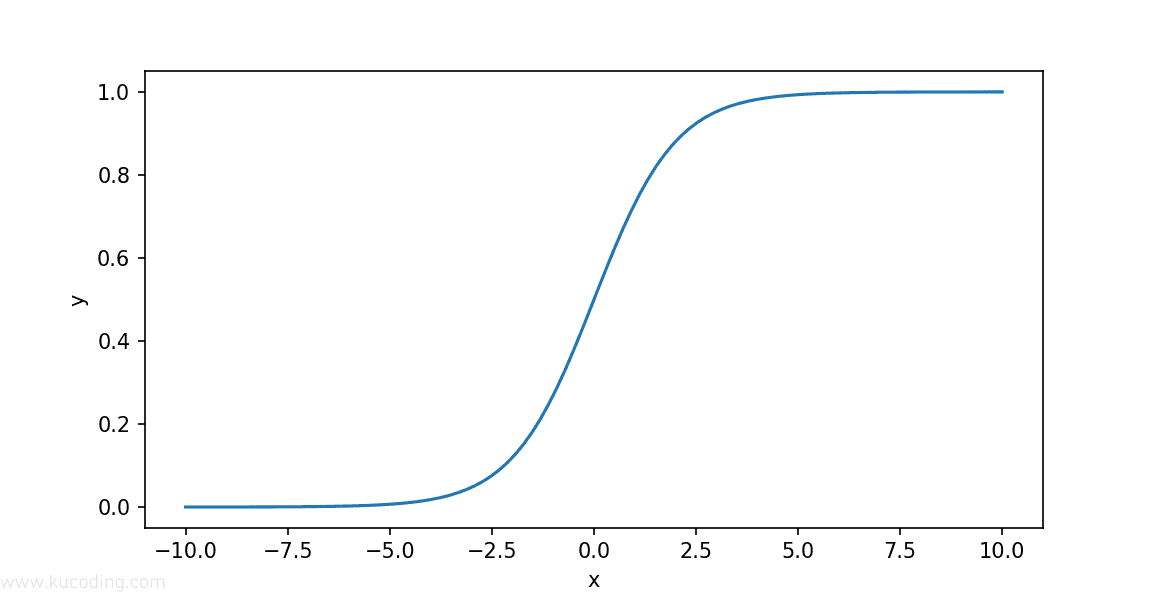
为了解决这类问题，我们就可以使用Sigmoid分布函数，它的定义如下：

$f(x)=\frac{1}{1+e^{-x}}$

它的图形长下面这样：

对应的代码实现如下：

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    sigmoid = 1 / (1 + np.exp(-x))
    return sigmoid


x = np.linspace(-10, 10, 100)  # 生成等间距 x 值方便绘图
plt.plot(x, sigmoid(x))
plt.xlabel("x")
plt.ylabel("y")
plt.show()

可以看到，这个函数呈现了非常完美的S形曲线，并且它的取值介于0和1之间，还关于$x=0$对称，x越大，y越趋近于1，越小，y越趋近于0。

这不正是$0-1$二分类问题完美选择！

4 逻辑回归模型

有了上面这个函数之后，我们就可以对前面的线性回归封装一层：

z_i=w_0x_0+w_1x_1+\dots+w_ix_i=w^Tx

$f(z_i)=\frac1{1+e^{-z_i}}$

此时，这里的z变量就等于线性回归的结果，它的范围是$( +\infty,-\infty)$，然后将其整体作为一个变量放入Sigmoid分布函数函数中，使得结果被压缩在了$(0,1)$之间。

这里的z可以被称之为分类边界，因为当z等于0时，两边对称，它的值决定了最终的分类。

将上面两个式子整理一下，结果如下：

$h_w(x)=\frac1{1+e^{-w^Tx}}$

由于它将被用于2分类问题，因此假定$y=1$的概率是$h_w(x)$，那么$y=0$的概率就是$1-h_w(x)$。

注意这里的假定，如果拿上面的示例来说，就是当样本数据的成绩为70，假定此时它的$h_w(x)$值是$0.7$，那么它最终被认定为1的概率就是0.7，被认定为0的概率为0.3。

这一步有点抽象，需要注意这里指的是一个样本最终结果被认定为1或0的概率。

因此可以表示为逻辑回归模型的概率分布：

$P(Y = y \mid x) = \begin{cases} h_w(x), & y = 1 \\ 1 - h_w(x), & y = 0 \end{cases}$

为了方便计算，我们会把上面的式子写为似然函数：

$P(y \mid x; w) = \left(h_w(x)\right)^y \left(1 - h_w(x)\right)^{1 - y}$

很容易验证这个式子的合理性，因为这里的y值只有0和1两个选项，分别代入进入就会发现和上面的式子是等价的。

由于这个式子中表示的是一个样本为1或0的概率，因此下一步我们就要计算所有样本中为1或0的概率：

$L(w) = \prod_{i=1}^{m} \left( h_w\left(x^{(i)}\right) \right)^{y^{(i)}} \left( 1 - h_w\left(x^{(i)}\right) \right)^{1 - y^{(i)}}$

实际上就是所有概率相乘。

由于连乘法表示起来比较繁杂，所以我们会对两边取对数，将其转换为连加的形式：

$\log L(w)=\sum_{i=1}^m\left[y^{(i)}\log h_w\left(x^{(i)}\right)+\left(1-y^{(i)}\right)\log\left(1-h_w\left(x^{(i)}\right)\right)\right]$

5 对数损失函数

上面的转换结果被称为对数似然函数，这个函数衡量了事件发生的总概率，因此只要求$L(w)$的最大值、得到此时$W$的估计值，那么就能得到所有样本中得到结果1的最大概率，相关理论分析：最大似然估计 - 知乎。

而在机器学习中，我们需要一个损失函数、通过求其最小值来进行参数优化，这两者正好相反。

因此将对数似然函数取个负，就从最大值变成了求最小值，满足损失函数的要求，同时对其求一个平均，得到平均损失：

$\log L(w)=-\frac1m\sum_{i=1}^m\left[y^{(i)}\log h_w\left(x^{(i)}\right)+\left(1-y^{(i)}\right)\log\left(1-h_w\left(x^{(i)}\right)\right)\right]$

之所以这里要新找一个损失函数、而不是用前面的平方损失函数，原因在于逻辑回归中的函数一般都不是凸函数，通过它找到的极值很可能只是局部的最大、最小值，而不是全局最大最小值。

而它之所以能作为损失函数，是因为它最终求出来的是一个等于1的平均概率结果，而不是真实结果，这个概率就可以被认定为损失，当这个损失尽可能小时，就意味着平均概率等于1的可能性就越大。

而什么时候损失概率最小呢？那就是当y值为1时、它预测出来的值百分百为1，y值为零时它预测出来的值百分百为0，只有这样平均损失才会最小：代入式子中损失就是0。

其对应的python代码为：

def loss(h, y):
    loss = (-y * np.log(h) - (1 - y) * np.log(1 - h)).mean()
    return loss

6 梯度下降法

有了损失函数后，下一步就是求它的极小值，使用的方法便是梯度下降。

这其实和大学学过的偏导理论有点关系，比如一个简单的两元一次函数：

$y=2x+3z$

分别将其中一个变量看作常量、对另一个变量进行偏导：

\frac{∂y}{∂x}=2 \frac{∂y}{∂z}=3

可以看到，这里的偏导结果实际上就是这条函数曲线对于变量x或z的变化速率，也就是高中时学的求导，当其值为0时，代表该变量在这个点变化速率为0，也就是到了极值点。

由于上面偏导之后为一个常数、永远不会为0，所以它便没有极值点。

而所谓梯度，就是由上面所有变量微分得到的一个方向向量：

∇y=(\frac{∂y}{∂x},\frac{∂y}{∂z})=(2,3)

这代表了这个函数在某个位置会向哪个方向变化多少。不仅仅只是分别向x、z这两个变量分别方向变化多少、而是两个的结合。

由于这里的梯度值依旧为常数、不可能为0，因此它依旧没有极值点。

有了简单的基础认知后，我们回到上面的式子，现在我们需要求它的极小值，也就意味着我们需要沿着梯度下降的方向寻找、找到它的值为0的地方，那么就代表此时它是一个极小值。

首先对前面的式子进行化简：

$\begin{aligned} \log(h_w(x^{(i)}) & =\log(f(w^Tx^{(i)})) \\ & =\log(\frac{1}{1+e^{-w^Tx^{(i)}}}) \\ & =-\log(1+e^{-w^Tx^{(i)}}) \end{aligned}$

\begin{aligned} \log(1-h_w(x^{(i)})) & =\log(1-\frac{1}{1+e^{-w^Tx^{(i)}}}) \\ & =\log(\frac{e^{-w^Tx^{(\boldsymbol{i})}}}{1+e^{-w^Tx^{(\boldsymbol{i})}}}) \\ & =\log(e^{-w^Tx^{(i)}})-\log(1+e^{-w^Tx^{(i)}}) \\ & =-w^Tx^{(i)}-\log(1+e^{-w^Tx^{(i)}}) \end{aligned}

将化简后的式子代入原式：

\begin{aligned} J(w) & =-\frac{1}{m}\sum_{i=1}^m\left[y^{(i)}(-\log(1+e^{-w^Tx^{(i)}}))+(1-y^{(i)})(-w^Tx^{(i)}-\log(1+e^{-w^Tx^{(i)}}))\right] \\ & =-\frac{1}{m}\sum_{i=1}^m\left[-\log(e^{w^Tx^{(i)}}+1)+w^Tx^{(i)}y^{(i)}\right] & (12)