1 介绍
上一章节我们通过逻辑回归的方式实现了对数据的分类，本章节我们更进一步，学习如何使用算法根据已有的分类数据对未知数据进行分类预测。
而K近邻算法（KNN）便是最简单且实用的一种方法，是由最近邻算法（NN）推广而来的。
最近邻算法原理相当简单，就是计算未知点到各个已经分类之间的距离，哪个距离最短、或者根据其它标准，就能对未知点进行分类。
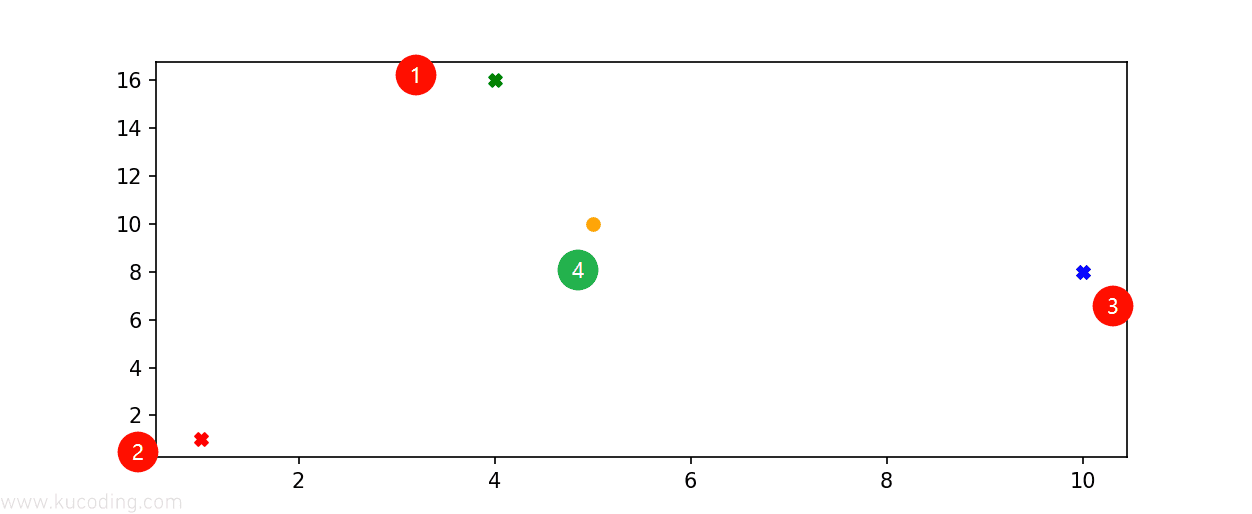
比如上图中，前三个X点代表已知的类型，那么对于未知的四，就可以通过分别计算它到其它三个点之间的距离来判断它的类型，距离谁更近，那么就预测它是什么类型。
但最近邻算法太过于绝对了，它只判断了哪个类别距离它最近、会导致分类效果不好。
而K近邻算法便是找出距离未知数据点最近的k个相邻样本，再根据这K个样本综合判断其类型。
2 距离计算
从上面我们已经了解到了，K近邻算法的关键就在于求点到点之间的距离，所以这里我们先来学习一下基本的距离算法。
而最常用的距离公式便是：曼哈顿距离和欧式距离。
这里我们以简单的二维数据点为例子，多维实际上也是在其上推演的，本质没区别。
假设我们有两个点：与。
那么曼哈顿距离指的就是：，也就是每个维度坐标差值的绝对值之和，它相当于求的是各个维度上两点的直线距离。
而欧式距离则更加符合我们的直觉，它求的是空间直线距离：，也就是每个维度坐标差值的平方和、最后开根号，实际上就是直角三角形的斜边长度计算公式。
将上面两个公式写为python代码如下：
def d_man(x, y):
d = np.sum(np.abs(x - y))
return d
def d_euc(x, y):
d = np.sqrt(np.sum(np.square(x - y)))
return d
注意这两个公式接收的是向量数据，里面是所有维度的值，逻辑是一样的。
3 K近邻算法实现
有了距离计算的基础之后，我们再来看看K近邻算法（KNN）的原理。
对于KNN算法来说，步骤实际上都是固定的、有以下四步：
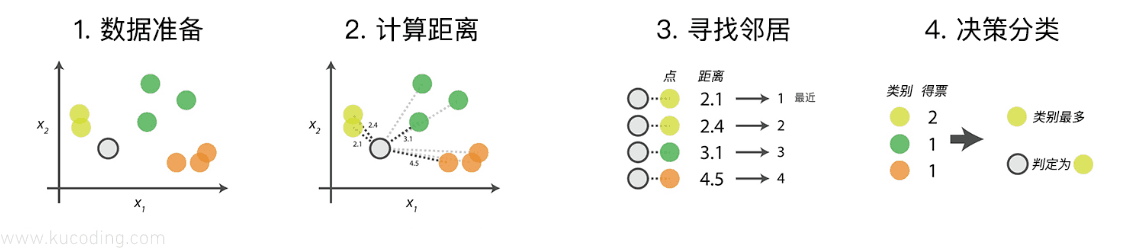
- 数据准备：通过数据清洗、处理，将其整理为向量，使其可以用来计算距离。
- 计算距离：计算测试数据与训练数据之间的距离
- 寻找邻居：找到与测试数据最近的K个训练数据
- 决策分类：根据规则，通过K个数据得到测试数据的类型。
首先是数据准备：
import numpy as np
import matplotlib.pyplot as plt
def gen_data():
features = np.array(
[
[2.9, 3.3],
[3.0, 2.7],
[3.2, 2.9],
[2.9, 2.7],
[2.8, 3.4],
[3.2, 3.3],
[3.2, 3.5],
[3.5, 2.9],
[3.9, 3.6],
[3.4, 3.3],
]
)
labels = ["A", "A", "A", "A", "A", "B", "B", "B", "B", "B"]
return features, labels
features, labels = gen_data()
x_feature = list(map(lambda x: x[0], features)) # 取出每个数据的x特征值组成新列表
y_feature = list(map(lambda y: y[1], features)) # 取出每个数据的Y特征值组成新列表
plt.scatter(x_feature[:5], y_feature[:5], c="b") # 在画布上绘画出"A"类标签的数据点
plt.scatter(x_feature[5:], y_feature[5:], c="g")# 在画布上绘画出"B"类标签的数据点
plt.scatter([3.2], [3.2], c="r", marker="x") # 待测试点的坐标为 [3.2,3.2]
plt.show()
运行效果如下：
其中前五个点与后五个点分别为两组数据，中间的x便是要进行预测分类的数据。
有了数据之后，然后我们就可以开始计算所有点到测试点之间的距离、并进行排序：
test = [3.2, 3.2]
dist = []
for i in range(len(features)):
dist.append((labels[i], d_euc(test, features[i])))
dist.sort(key=lambda x: x[1])
有了所有点的距离后，假设选择K为5，使用多数表决的方式，也就是选择距离测试样本点最近的5个点，哪种类型最多、就认为测试数据是哪种类型：
k_distance = dist[:5]
a_num = 0
b_num = 0
for i in k_distance:
if i[0] == "A":
a_num += 1
else:
b_num += 1
