朴素贝叶斯算法实现垃圾分类实战详解-大模型实战入门

1 介绍

分类预测中，以概率论作为基础的算法较少，而朴素贝叶斯便是其中一种，它实现简单、预测分类的效率还很高，因此使用频率也很高。

由于它基于概率论，因此这里首先来了解一下概率论的基础。

如果事件A发送的概率表示为 $P(A)$ ，事件B发生的概率为 $P(B)$ ，那么事件A、B同时发生的概率我们就可以表示为 $P(AB)$ 。

在该基础之上，如果我想要求当事件B发生之后A发生的概率为多少，就被称为条件概率，其计算公式为： $P(A \mid B)=\frac{P(AB)}{P(B)}$ 。

有了B事件发生之后A事件发生的概率公式，那么如果求 $P(B|A)$ 呢？也就是在A事件发生之后的B事件发生的概率？

这便是贝叶斯定理，其推导过程如下：

$P(B \mid A)=\frac{P(AB)}{P(A)}$

$P(AB)=P(A\mid B)\times P(B)$

结合上面两个式子得到完整的贝叶斯定理：

$P(B \mid A) = \frac{P(AB)}{P(A)}=\frac{P(A \mid B)\times P(B)}{P(A)}$

其中 $P(A)$ 、 $P(B)$ 这种已知的概率，称为先验概率，它是通过过往经验和分析得到的概率，比如抛硬币我们会认为其概率就是0.5。

当事件发生之后求的反向概率，则被称为后验概率，比如上式中的 $P(B \mid A)$ 就是通过 $P(A)$ 和 $P(B)$ 先验概率求出来的反向条件概率。

而朴素贝叶斯的原理就是将贝叶斯原理与条件独立结合而成的算法：

P(类别 \mid 特征) = \frac{P(特征 \mid 类别)\times P(类别)}{P(特征)}

相当于就是将A换为了特征、B换为了类别。

那么我们现在就可以通过这个公式求出当特征概率已知的情况下，它类别概率是什么，这不正好满足我们分类的需求嘛！

其中右边类别的概率、特征的概率、特征在类别下的概率都是已知的。

朴素贝叶斯中的朴素，含义就是假设预测的各个属性之间相互独立、每个属性独立的对分类结果产生影响。

比如判断一朵花的类型有叶长、花瓣数量两个特征，那么前面我们预测的方式都是结合这两者一起来预测花朵的类型，而在朴素贝叶斯中，就认为这两个特征是独立的影响类别判断、而不会将其结合在一起判断。

这样做使得其变得简单而简洁，但自然的，在某些情况下就会牺牲一定的分类准确度。

2 朴素贝叶斯算法实现

有了上面的基础，下面我们就可以来介绍朴素贝叶斯算法的python代码实现逻辑了。

流程如下：

假设X=\left\{x_1,x_2, \dots ,x_n\right\}为训练数据，而 $x_i$ 是训练数据的特征值。
假设Y=\left\{y_1,y_2,\dots,y_m \right\}为类别集合
计算每种类别在特征值条件下的概率：P(y_1\mid x),P(y_2\mid x),\dots,P(y_m\mid x)
寻找P(y_1\mid x),P(y_2\mid x),\dots,P(y_m\mid x)中最大的概率 $P(y_k\mid x)$ ，则x就属于类别 $y_k$

而根据前面朴素贝叶斯算法原理，这里比较所有的 $P(y_i\mid x)$ 大小，实际上比较的是P(类别_i \mid 特征)，由于根据上面的转换公式，它等于：\frac{P(特征 \mid 类别)\times P(类别)}{P(特征)}

所有的P(特征)分母值都相同，所以相当于就是比较分子P(特征 \mid 类别)\times P(类别)的乘积大小。

那么如何计算得到这两个值呢？这就需要用到极大似然估计法与贝叶斯估计法了。

为了更加直观的看到效果，这里先给出一组测试数据：

def gen_data():
    # 生成示例数据
    data = {
        "x": ["g", "g", "r", "r", "b", "g", "g", "r", "b", "b", "g","r", "g", "r", "b"],
        "y": ["m", "s", "l", "s", "m", "s", "m", "s", "m", "l", "l", "s", "m", "m", "l"],
        "labels": ["A", "A", "A", "A","A", "A", "A", "A", "B", "B", "B", "B", "B", "B", "B"],
    }
    return data

这里的测试数据中，x、y为两个特征值，也就是 $X=\{x,y\}$ 。labels则是一个类别，也就是 $Y=\{labels\}$ 。

2.1 极大似然估计

所谓极大似然估计，就是根据过往经验，推断出最有可能造成某个结果的参数值。

比如A箱子里面有999个白球、一个黑球，B箱子里面有999个黑球、一个白球。

那么当我说我抽出了要给白球时，你自然而然的就会认为我是从A箱子里面抽出来的，因为A箱子里面抽出白球的概率实在是太大了。

回到这里，我们求P(类别)时，可以认为它的概率就是它在训练数据中所有类别的占比，比如这里训练数据中的labels为其中一个类别，由于数据总共有15条，其中A占8条，B占7条，那么就能求出各自的概率分别为 $\frac{8}{15}$ ， $\frac{7}{15}$ 。

此时对应的python代码为：

def get_P_labels(labels):
    labels = list(labels)  # 转换为 list 类型
    P_label = {}  # 设置空字典用于存入 label 的概率
    for label in labels:
        # 统计 label 标签在标签集中出现的次数再除以总长度
        P_label[label] = labels.count(label) / float(
            len(labels)
        )  # p = count(y) / count(Y)
    return P_label

而对于P(特征 \mid 类别)来说，要求的实际上就是在某种类别情况下，某个特征出现的概率。

比如属于A标签的8个数据中，对于X特征来说，g就占了4个，所以对于A标签、X特征来说，g的概率就是 $\frac{4}{8}$ 。

对应的python代码示例求A标签三个特征值的概率如下：

def get_A_X_fea_lab(data):
    ret={
        'r':0,
        'g':0,
        'b':0
    }
    for i in range(0,8):
        ret[data['x'][i]]+=1
    ret['r']/=8
    ret['g']/=8
    ret['b']/=8
    return ret

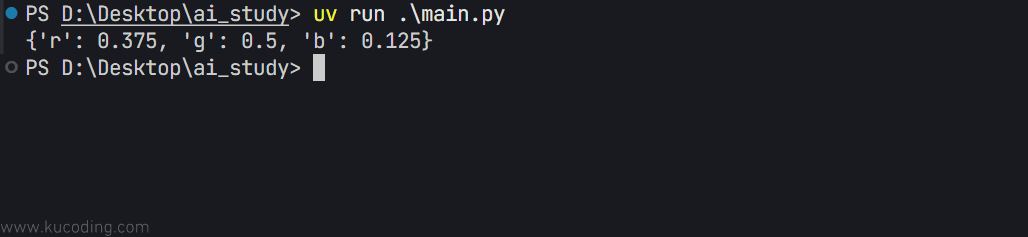
ret=get_A_X_fea_lab(data)
print(ret)

结果：

2.2 贝叶斯估计

在最大似然估计中，一旦某个类别缺少某个特征，就会出现概率为0的情况。

比如当上方A标签内恰好没有X特征的b特征值，那么在b特征下A的概率就直接成为了0，着显然偏离的很厉害，毕竟这些信息都应该成为分类的标准。

而解决这样问题的方式就是采用贝叶斯估计，其底层逻辑其实就是为每个特征的特征值都加上下限，保证其不可能为0。

比如还是A标签的8个X特征数据中，g占了4个，按最大似然估计值就是 $\frac{4}{8}$ ，那么按贝叶斯估计就是 $\frac{4+1}{8+1*3}=\frac{5}{11}$ 。

这里分子加的1可以用变量 $\lambda$ 表示，此时分母加的 $1*3$ 就变成了 $\lambda*k$ ，这里的k实际上就是X特征内值的类型个数有三个：r、g、b，所以值为3。

这便是贝叶斯估计，它可以保证所有概率计算结果都不可能为0，当 $\lambda$ 的值为0时，就是最大似然估计，一般我们取 $\lambda$ 的值为1，此时又被称为拉普拉斯平滑。

此时可以将上面的oython代码改写为：

def get_A_X_fea_lab(data):
    ret={
        'r':0,
        'g':0,
        'b':0
    }
    for i in range(0,8):
        ret[data['x'][i]]+=1
    ret['r']=(ret['r']+1)/(8+3)
    ret['g']=(ret['g']+1)/(8+3)
    ret['b']=(ret['b']+1)/(8+3)
    return ret

ret=get_A_X_fea_lab(data)
print(ret)

2.3 常见模型

在实际数据中，我们可以根据特征的数据类型不同，使用不同的模型来计算先验概率，主要分为：多项式模型、伯努利模型、高斯模型。

其中多项式模型常用于特征值离散的情况，比如上面的示例中特征值就是离散的。

伯努利与多项式模型一样，也适用于离散模型，但不同之处在于，此时每个特征的取值只能为1或0。

最后高斯模型则是用于处理连续的特征变量，因为一旦连续，就代表其类型无限多。

6. 朴素贝叶斯算法实现垃圾分类实战详解

1 介绍

2 朴素贝叶斯算法实现

2.1 极大似然估计

2.2 贝叶斯估计

2.3 常见模型

文章目录